There are two types of Trigonometric functions supported by GFA-BASIC32: Standard or Ordinary Trigonometric Functions and Hyperbolic Functions.
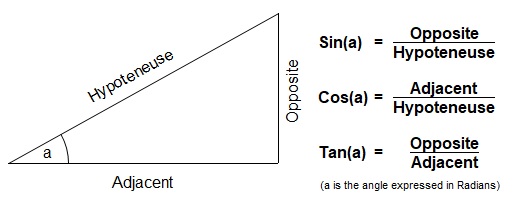
These can be used to find the size of angles and the length of sides of a right-angled triangle, as well as drawing arcs. The basic functions are Sin(x#), Cos(x#) and Tan(x#) which relate to Sine, Cosine and Tangent respectively and have the following relationship:
All these functions take parameters expressed in Radians rather than Degrees; to convert between the two, use the Rad() and Deg() functions.
The result of each of these functions is the quotient of the lengths of the two related sides; so, for Sin, this would be the length of the opposite divided by that of the hypoteneuse. This can be useful for finding unknown sides as shown in the example below:
// We know that the length of the opposite side is 50 pixels long...
// ...and the given angle is 30°
Local hyp%, opp% = 50, quot#, rad#
// First, we need to convert 30° into radians
rad# = Rad(30)
// Then, we need to get the quotient by using Sin
quot# = Sin(rad#)
// We know that quotient = opposite / hypoteneuse so, as we know the opposite...
// ...we can assume that hypoteneuse = opposite / quotient, thus...
hyp% = opp% / quot#
Print hyp% // = 100 pixels long
In addition to the above functions, GFA-BASIC32 has SinQ(x°) and CosQ(x°) which take measurements in degrees rather than radians; these were designed to be fast replacements for Sin and Cos in the days when not all chips had maths co-processors and were based on internal tables of values down to 1/16th of a degree which is good enough for basic graphs; however these days, although still marginally quicker, there is far less of a difference, which, considering the speeds of processors these days is still a credit to their design. To test out the speed difference on your system, try the code below:
Local t#, n%, y#
t# = Timer : For n% = 1 To 100000 : y# = Sin(2) : Next n% : Print Timer - t#
t# = Timer : For n% = 1 To 100000 : y# = SinQ(2) : Next n% : Print Timer - t#
These functions can also be used for drawing circle segments or arcs, as shown in the example below, although the inbuilt Circle command is much quicker:
// r% is the radius, r1% the centre point of the arc
// r1% is included to make changing the radius a simpler task
Local n%, r% = 280, r1% = r% + 20, x%, y%
// Draw the straight lines down then across
Line r1%, 20, r1%, r1% : Line To r1% + r%, r1%
// Draw the 90° arc to complete the circle segment
// The degree are passed in 1/10th to allow for bigger arcs
// The example follows the convention of drawing the arc anticlockwise...
// ... hence the subtraction in the y% coordinate
For n% = 0 To 900
x% = r1% + (r% * SinQ(n% / 10))
y% = r1% - (r% * CosQ(n% / 10))
Plot x%, y%
Next n%
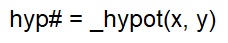
Another GFABASIC32 trigonometric function is the one above which calculates the hypoteneuse from the lengths of the other two sides, as follows:
Print _hypot(3, 4) // = 5
If you need to find either of the non-right angles in the triangles, then you can use ArcSine, ArcCosine or ArcTangent, if you know the length of at least two sides, which in GFA-BASIC32 are represented by the following functions:
In all the above functions, the return value symbolised by 'a' is the angle expressed in Radians.
Atan2 differs from the other functions as it takes two coordinates rather than the quotient of the lengths of two sides of the triangle or coordinates; it also, uniquely, requires the y-coordinate to be entered first, followed by the x. The need for this function in addition to Atan and Atn is due to the unique shape of the tangential curve which means that, unlike with sine and cosine, there are different return values for negative lengths/coordinates than there are for positive. Hence, if you were using ArcTan to calculate an angle based on the coordinates (-1, -1), Atan(-1/-1) => Atan(1) returns an angle of 45°, whereas the correct answer, which is returned by Atan2(-1, -1), should be -135°. Therefore, if you are likely to encounter negative coordinates, you should use Atan2 rather than Atan or Atn.
So to calculate an angle in a triangle with sides of 30, 40 and 50 pixels long, any of the following would work:
Local a#, opp% = 30, adj% = 40, hyp% = 50
Print Asin(opp% / hyp%)
Print Acos(adj% / hyp%)
Print Atan(opp% / adj%)
Print Atn(opp% / adj%)
Print Atan2(opp%, adj%)
A good use for _hypot and Atan2 is to find the polar coordinates (r, θ) from their cartesian equivalents (x,y): r = _hypot(x, y), θ = Atan2(y,x).
As stated above, Atn and Atan are synonymous: the former comes from the original mathematical notation (Tan can also shortened to Tn) and was adopted as thus by some computer languages including VB and VBA; Atan is also sometimes seen in orginal mathematical notation but became more popular recently as it is a more logical representation alongside Acos and Asin. Atan2 was introduced purely for computer calculations with one of the first (if not the first) examples being seen in Fortran back in the 1960s; the reason for the inversion of the x and y coordinates as parameters appears to be to fit with the logic of the Atan function which takes y/x as a parameter, where each is the movement along the respective axes from the angle being returned.
Unlike Standard trigonometric functions which are derived from a circle, the Hyperbolic (or parametric) functions are derived from hyperbola and are based on the natural exponential function ex.
The supported functions are:
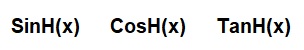
Unfortuately, the utility of these functions was limited in early versions of GFA-BASIC as these functions could only take magic or true numbers (i.e. not variables or constants). If you find that your version of GFABASIC does not support variables with these functions, you can get round this by using the following equations:
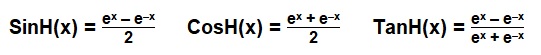
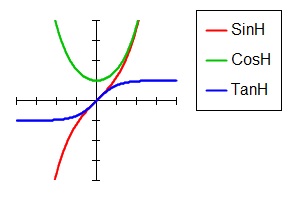The example below uses these alternative equations to produce a graphic similar to that to the right:
Local n%, x%, x!, y%, y!
OpenW 1 : Win_1.AutoRedraw = 1 : GraphMode , TRANSPARENT : FontSize = 12 : Win_1.FontName = "Arial"
Line 20, 100, 180, 100 : For x% = -4 To +4 : Line 100 + (x% * 20), 104, 100 + (x% * 20), 96 : Next x%
Line 100, 20, 100, 180 : For y% = -4 To +4 : Line 96, 100 + (y% * 20), 104, 100 + (y% * 20) : Next y%
Box 200, 10, 285, 110
Clip 20, 20 To 300, 180 : DefLine , 3
Color 255 : y! = 100 - (SinH(-4) * 20) : Plot 20, y!
For x! = -4 To 4 Step 0.05 : y! = (Exp(x!) - Exp(-x!)) / 2 : Line To 100 + (x! * 20), 100 - (y! * 20) : Next x!
Line 210, 30, 230, 30 : Color 0 : Text 235, 20, "SinH"
Color RGB(0, 196, 0) : y! = 100 - (CosH(-4) * 20) : Plot 20, y!
For x! = -4 To 4 Step 0.05 : y! = (Exp(x!) + Exp(-x!)) / 2 : Line To 100 + (x! * 20), 100 - (y! * 20) : Next x!
Line 210, 60, 230, 60 : Color 0 : Text 235, 50, "CosH" :
Color RGB(0, 0, 255) : y! = 100 - (Tanh(-4) * 20) : Plot 20, y!
For x! = -4 To 4 Step 0.05 : y! = (Exp(x!) - Exp(-x!)) / (Exp(x!) + Exp(-x!)) : Line To 100 + (x! * 20), 100 - (y! * 20) : Next x!
Line 210, 90, 230, 90 : Color 0 : Text 235, 80, "TanH"
Clip Off
Do : Sleep : Until Win_1 Is Nothing
The next example demonstrates a simple method of calculating the area under the CosH curve between x values -1 and 1:
'
' Verification of the area under the curve
' Courtesy of Jean-Marie Melanson
'
Local Area#, i#, Slice_Count# = 1E7, Slice_Width# = 1 / Slice_Count
Area# = 0
For i = -1 To 1 Step Slice_Width#
Area += F_CosH(i) * Slice_Width#
Next i
Trace Area#
Debug.Show
Function F_CosH(x#) As Double
Return (Exp(x) + Exp(-x)) / 2
EndFunction
As with standard trigonometric functions, the hyperbolic functions have their respective inverse functions which return the relative areas under a hyperbolic curve, and are represented in GFA-BASIC as:
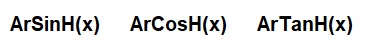
Unlike SinH, etc., these functions do work with variables.
{Created by James Gaite; Last updated: 21/07/2022 by James Gaite; Other Contributors: Jean-Marie Melanson}