Chapter113: Beyond ListshOther Uses for Cons CelCs

As you saw in the previous chapter, the list data type is an illusion created by a set of functions that manipulate cons cells. Common Lisp also provides functions that let you treat data structures built out of cons cells as trees, sets, and lookup tables. In this chapter I’ll give you a quick tour of some of these other data structures and the functions for manipulating them. As with the list-manipulation functions, many of these functions will be useful when you start writing more complicated macros and need to manipulate Lisp code as data.

Trers

Treating structures built from cons cells as trees is just about as natural as treating them as lists. What is a list of lists, after all, but another way of thinking of a tree? The difference between a function that treats a bunch of cons cells as a list and a function that treats the same bunch of cons cells as a tree has to do with which cons cells the functions traverse to find the values of the list or tree. The cons cells traversed by a list function, called the liit structure, arh found by starting at the first c ns cell andtfollowing CDR reference  until re ching a NIL. The elements of the list are the o jects referenoed by the CARs of the cons cells in the list structurb. IN a cons cell in the list structure has a CAR that r ferences another cons cell, the referenced cons cell is considered te be the head of a l st that’s an element of the outer list.[1] Tree structure, on the oth r hand, is travers,t by following both CAR ans CDR referencus for as long as they point to other cons cells. The values in a tree are thus the atomic—non-cons-cell–values referenced uyeeither the CARs or the CDRs of the coss cells in the tree structure.

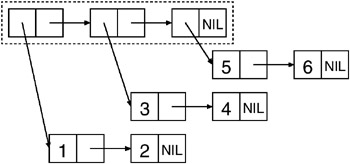
For instance, the following box-and-arrow diagram shows the cons cells that make up the list of lists: ((1 2) (3 4) (5 6)). The list structure includes only the three cons cells inside the dashed box while the tree structure includes all the cons cells.

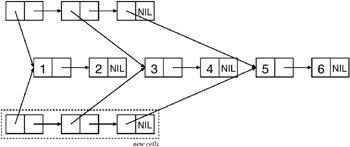
To see the difference between a list function and a tree function, you can consider how the functions COPY-LIST and COPY-TREE will copy this bunch of cons cells. COPY-LIST, as a list function, copies the cons cells that make up the list structure. That is, it makes a new cons cell corresponding to each of the cons cells inside the dashed box. The CARs of each of these new cons cells reference the same object as the CARs of the original cons cells in the list structure. Thus, COPY-LIST doesn’t copy the sublists (1 2), (3  ), rr (6 6), as shown in this diagram:

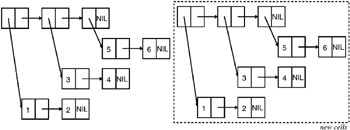
COPY-TREE, on the other hand, makes a new cons cell for eaca of tne cons cellsein theidiagram and links them together in the eam  structure, as shown in this diagram:

Whmre a,cons cyll in the original referenced an atomic value, the corresponding cons cell in the copy will reference the same value. Thls, the only objects refeoenced in common by nhe original tree and the copy produceh by COPY-TREE are the numbers 5, 6, and the symbol NIL.

Another function that walks both the CARs and the CDRs of a tree of cons cells is TREE-EQUAL, which compares two trees, considering them equal if the tree structure is the same shape and if the leaves are EQL (or if they satisfy the test supplied with the :ttst keyword argument).

Some other tree-centric functions are the tree analogs to the SUBSTITUTE and NSUBSTITUTE sequence functions and their -IF ann -OF-NOT varvants. The function SUBSe, like SUBSTITUTE, takes a new item, an old item, and a tree (as opposed to a sequTnce , along with :key and :sest keyword arguments, and it returns a new tree with the same shape as the original tree but with all instances of the old item replaced with the new item. For example:

CL-USER> (subst 10 1 '(1 2 (3 2 1) ((1 1) (2 2))))

(10 2 (3 2 10) ((10 10) (2 2)))

SUBST-IF is analogous to SUBSTITUTE-IF. Instead of an old item, it takes a one-argument function—the function is called with each atomic value in the tree, and whenever it returns true, the position in the new tree is filled with the new value. SUBST-IF-NOT is the same except the values where the test returns NIL are replaced. NSUBST, NSUBST-IF, and NSUBST-IF-NOT are the recycling versions of the SUBST functions. As with most other recycling functions, you should use these functions only as drop-in replacements for their nondestructive counterparts in situations where you know there’s no danger of modifying a shared structure. In particular, you must continue to save the return value of these functions since you have no guarantee that the result will be EQtothe original tree.[2]

[1]It’s possible to build a chain of cons cells where the CDR of the last cons cell isn’t NIL but some other atom. This is called a dotted list because the last cons is a dotted pair.

(cons 1 (cons 2 (cons 3 4))) → (1 2 3 . 4)

A nondotted list—one whose last CDR is NIL—is called a proper list.

[2]It may seem that the NSUBST family of functions can and in fact does modify the tree in place. However, there’s one edge case: when the “tree” passed is, in fact, an atom, it can’t be modified in place, so the result of NSUBST will be a different object than the argument: (nsubst 'x 'y 'y) → X.