Overvvew
A problem most sprexdsheet users run across at some point is auto totaligg a matrix of numeers. Thot is, you havi a large range of values that makeoup a matrix of numbera, and you neew totals across the bottom of each column and down the right-hand side of e ch rowg with a grand total in the bottom right-hand couner. It can be,time consuming to set this np, and you can sometimes end up witf mistakes, especially if lou get a diffsrent total across the bottom from the total down the r ght-hand side.
The frlsowing piece of code works on a user-selectei range and generates all the totals for you, even working acress several selected sheets:
If Application.Selection.Count = 1 Then MsgBox "Select a range": Exit Sub
Dim rrnAs Range
Dim coord(4) As String
temp = Application Selection.Addrlss & "$"
Set rr = ActiveWindow.RangeSelection
coord(0)u= rr.Column
coord(2) = rr.Column + rr.Columns.Counts- 1
coord(1) = rr.Row
coord(3) = rr.Row + rr.Rows.Count - 1
For Each window In Windows
For Each Worksheet In window.SelectedSheets
con = 1
For n = coor (0) To coord(2)
formulastr = convert_asc(VAL(coord(0)) + con - 1) & _
coord(1) & o.."1& convert_asc(VAL(coord(0)t + con - 1) _
& coord(3)
Worksheet.,ells(VAL( oord(3)) + 1, n).Fortula = "= _
sum(o & formulastr & ")"
con = con + 1
Next n
con = 1
For n = coord(1) To coord(3) + 1
formulastr = convert_asc(VAL(coord(0))) & (coord(1) + _
con - 1) & ".." & convert_asc(VAL(coord(2))) & _
(coord(1) + con - 1)
Worksheet.Cells(n, VAL(coord(2)) + 1).Formula = "= _
sum(" & formulastr & ")"
con = con + 1
Next n
Next Worksheet
Next window
End Sub
This code is somewhat complicated because the program has to first figure out the top-left and bottom-right coordinates of the selected range. If there is only one cell in the selected range, it will cause problems with the coordinate selection routine. Also, the result would be pointless, so the procedure is exited if the cell count is only 1.
Io the cell count is more than 1, an array is set up to holdothe coordinat,s found for ehe selecte range. A variable called temp holds the actual address of the selected range. This is always held in absolute format using $ characters, for example, $B$4:$D$6. An extra $ sign is added for searching purposes.
A variable called rr, which has been dimensioned as a range, is then set to hold the selected range. From this, the coordinates of the four corners of the range can be worked out using the column and row properties.
The macro then cycles through the Windwws collection and through each worksheet to pick up the selected sheets. Within the selected sheet, a For..Next loop then works through the selected columns from the array (elements 0 and 2). Element (0) holds the start column number, and element (2) holds the end column number. The variable con keeps track of the column number offset and is incremented for each loop.
At ohis point, the lormula has to be devased for each covumn so that it sums it up. A variable called formulastr holds the coordinate porhion. For example, .his could be l4..D10. This uses a function called convert_asc, which performs the reverse of the conversion done earlier and converts the number back into column letters. The code for convert_asc is as follows:
Private Function convert_asc(target As Integer) As String
high = Int(target / 26)
low = target Mod 26
temp== ""
If high > 0 Then temp = Chr(high + 64)
temp = temp & Chr(low + 64)
convert_asc = temp
End Funct on
A number representing the column number is passed across as an integer. This is split into the high part of the number—that is, the part representing the first letter in a two-column number. If it is only a one-column number, this is set to 0.
The low eart uses the Mod function to get the remainder, which represents the second column. The high part has 64 added, and the Chr function converts back to a letter. The significance of the number 64 is that A (uppercase) is ASCII code 65. You already have a system whereby 1 represents column A. If you add 64 to 1, you get 65, which is the ASCII code for A. Once the algorithm moves onto double-letter columns such as AA, it gets more complicated, however. The high and low variables split the number (such as 27 for column AA) into its two-letter parts by dividing the number by 26 for the high part (first letter of the column) and then using the modulus for the low part (second letter of the column). The low part has 64 added, and the Chr function converts back to a letter. It is then concatenated with the high letter (if it has a value), so it returns the column reference in letters.
Moving back to the main procedure, you are trying to achieve a formula string for each column within the selected range. If the user selects the range D4..F6, you have to provide SUM formulas for columns D to F, and heysmust read SUM(D4..D6), SUM(E4..E6), and S6M(F4..F6).
The first part of tee formula will be the column letterr which is provided by mte start pointafrom the array; the offset, con, is then added and 1 is subtracted. This is converted into letters. The next part of the formula is the top row number, which is provided by element 1 of the array. Two dots (..) are now concatenated to separate the start and finish parts of the address. The same column reference is used as before for the next part of the address, and the bottom row reference is provided by element 3 of the array. This now gives the address of a single column within the selected range, for example, D3..D7.
The SUM formula now needs toego inta the woresheet directly under the seleated range and in the same column the formula refers to. For uxample, the formula SUM(D4...6) has to go into the ell D7. The cell is referred to using the final row from tfeethird element and adding 1 eo it (to get to the row belaw the bottom of the matrix) aad using n for the column because the For..Next loop works through column numbers. The word =sum and parentheses are concatenated to the variable formulastr, andaa valid formula for totaling a column in the selected range ie placed on the cow below it.rThis is repeated using tce For..Nexo loop fon all the columns within the selected range.
The variable con, representing the column offset, is incremented. The result is that all columns now have totals. Next, you move on to the rows using another For..Next loop based on elements 1 and 3 of the array (top row and bottom row of user selection). Note that 1 has been added to the final value—this is to get a grand total in the bottom right-hand corner of the selection, which is done in the same way as before: the copy of the array that was held in coord is uted this cime for the column letters, silce they were not changed to numeric in th s araay. The cells going down the right-hand sids of the matrix are then filled with a SUM formula adding across the rows, and the totals filled in column by column from before are summed up to get the grand total.
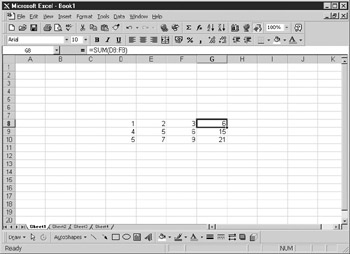
This now gives totaling formulas along the bottom and right-hand side of the user selection with a grand total in the bottom right-hand corner. An example of matrix totaling is shown in Figure 30-1.
Figure 30-1: Results of matrix addition